Asymmetric Encryption
- Asymmetric Encryption
- Digital Signature
- Asymmetric Encryption Methods
- ECC Variations
- Diffie-Hellman
- Diffie-Hellman Groups
Asymmetric Encryption
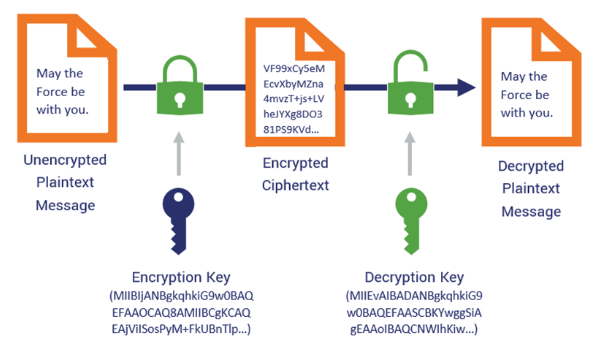
Asymmetric encryption uses a pair of keys: a public key for encryption and a private key for decryption.
- **Public key encrypts data**, and only the corresponding private key can decrypt it.
- **Private key decrypts the data**, can be used to sign data, which the public key can verify.
This dual-key system allows for secure communication, digital signatures, and secure key exchange without requiring shared secrets.
Digital Signature
A digital signature is a cryptographic method for verifying the authenticity and integrity of digital messages or documents.
- Uses a private key to create the signature and a public key to verify it.
- The signature confirms the sender’s identity, ensures the message hasn’t been altered, and provides proof that the signer can’t deny signing.
How It Works
- A hash function creates a fixed-size hash from the message.
- The private key is used to sign the hash, creating the digital signature.
- The public key is used to verify the signature and check the message’s integrity.
Benefits
- Authentication: Confirms the identity of the signer.
- Integrity: Ensures the message hasn’t been changed.
- Non-Repudiation: Prevents the signer from denying their signature.
Use Cases
- Email Encryption: Verifies email sources.
- Software Distribution: Confirms software integrity.
- Legal Documents: Validates digital contracts and agreements.
- Blockchain and Cryptocurrency: Secures transactions.
Asymmetric Encryption Methods
Each algorithm supports a range of key sizes that directly influence the security and efficiency of encryption and key exchange. Generally, larger key sizes offer more security but require more computational resources.
RSA and DSA:
- RSA is the most widely used, offering compatibility with a range of systems.
- DSA is optimized for digital signatures.
ECC:
- Mostly used in mobile devices and low-power computing devices.
- Provides similar security with smaller key sizes, leading to efficiency gains.
- ECC with a 256-bit key is just as secure as RSA with 2048-bit key.
Summarized table:
| Algorithm | Key Structure | Supported Key Sizes | Use Cases | Strengths | Weaknesses |
|---|---|---|---|---|---|
| RSA | Public-private key pair | 1024-4096 bits | Secure communication, digital signatures | Established, widely used; supports large key sizes | Slower than symmetric methods; susceptible to certain attacks with smaller keys |
| ECC (Elliptic Curve Cryptography) | Public-private key pair | 160-521 bits | Secure communication, digital signatures | Smaller key sizes; heavily used in mobile devices | More complex mathematical basis; not as widely adopted as RSA |
| DSA (Digital Signature Algorithm) | Public-private key pair | 1024-3072 bits | Digital signatures, authentication | Fast for signature generation; widely accepted | Slower for verification; requires secure parameter selection |
| Diffie-Hellman | Key exchange | 1024-8192 bits | Secure key exchange, establishing shared keys | Enables secure key exchange over insecure channels | Does not provide encryption or authentication by itself |
ECC Variations
Elliptic Curve Cryptography (ECC) is a type of public-key cryptography that relies on the mathematical properties of elliptic curves to secure communications. Within ECC, there are several variations that offer different approaches and benefits.
ECDSA
- ECDSA (Elliptic Curve Digital Signature Algorithm)
- A variant of the Digital Signature Algorithm (DSA) that uses elliptic curves for digital signatures.
- Often used in secure communications, blockchain technology, and software signing.
- Provides strong security with smaller key sizes compared to RSA.
- Efficient for generating digital signatures.
- Requires careful selection of curve parameters and robust implementation to avoid vulnerabilities.
ECDH
- ECDH (Elliptic Curve Diffie-Hellman)
- A variation of the Diffie-Hellman key exchange that uses elliptic curves.
- Used to establish shared secret keys for secure communication.
- Offers secure key exchange with reduced computational overhead compared to traditional Diffie-Hellman.
- Like ECDSA, requires careful parameter selection to ensure security.
ECMQV
- ECMQV (Elliptic Curve Menezes-Qu-Vanstone)
- An elliptic curve-based key agreement protocol.
- Used in situations requiring authenticated key exchange.
- Provides authenticated key exchange with lower computational requirements than traditional MQV.
- Less commonly used than ECDSA or ECDH.
- Robustness depends on correct parameter choices and secure implementation.
EdDSA
- EdDSA (Edwards-curve Digital Signature Algorithm)
- A digital signature algorithm based on the Edwards curve family.
- Increasingly used in modern cryptographic systems for digital signatures.
- High security and simplicity; resistant to several types of attacks, with rapid signature verification.
- Relatively new, but gaining adoption due to its efficiency and security characteristics.
Secp256k1
- A specific elliptic curve used in ECC.
- Widely used in blockchain and cryptocurrency applications, notably in Bitcoin.
- Offers a strong level of security with smaller key sizes, optimized for efficient computation.
- Selection of this curve over others is driven by specific community choices
- Less versatile outside blockchain applications.
Diffie-Hellman
Diffie-Hellman is a cryptographic protocol for secure key exchange, enabling two parties to establish a shared secret over an insecure communication channel.
- Establishes a shared secret key without directly sharing it.
- Based on discrete logarithms and modular arithmetic.
- Shared secret can’t derived easily by attackers due to complex math.
- An asymmetric algorithm, but doesn’t provide the actual encryption.
- It is key exchange protocol,
Use Cases:
- Often used to set up shared encryption keys.
- Used when setting up VPN tunnels or other encryption tunnels.
- Applied in SSL/TLS, IPsec, and VPNs.
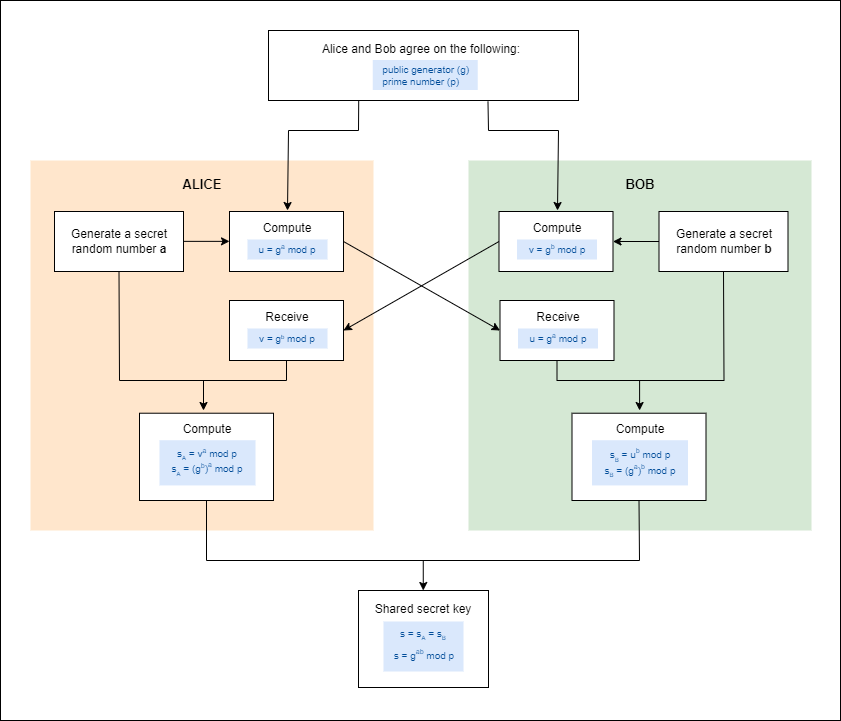
How It Works:
- Both parties agree on a base (generator) and a prime modulus.
- Each party chooses a private key.
- Public key is derived by raising the base to the power of the private key, modulo the prime.
- The public keys are then exchanged.
- Each party calculates the shared secret using the other’s public key and their own private key.
Example:
- Parties agree on a common base ( g ) and a prime modulus ( p ).
- Alice chooses a private key ( a ) and sends ( g^a \mod p ) to Bob.
- Bob chooses a private key ( b ) and sends ( g^b \mod p ) to Alice.
- Alice calculates ( (g^b \mod p)^a ) to get the shared secret.
-
Bob calculates ( (g^a \mod p)^b ) to get the same shared secret.
Strengths:
- Secure key exchange without revealing the key
- Resistant to eavesdropping and man-in-the-middle attacks when implemented correctly.
Weaknesses:
-
Vulnerable to attacks like the man-in-the-middle if proper authentication is not implemented
-
Depends on the difficulty of solving the discrete logarithm problem.
-
To be truly secure, it should be combined with additional mechanisms
Diffie-Hellman Groups
Diffie-Hellman groups are pre-defined sets of parameters used in the Diffie-Hellman key exchange protocol. These groups consist of a generator (a base number) and a prime modulus, which are critical for the mathematical operations that allow two parties to create a shared secret.
| Group Name | Prime Modulus Size (bits) | Typical Use Cases | Notes |
|---|---|---|---|
| Group 1 | 768 | Legacy applications | Considered insecure, rarely used today |
| Group 2 | 1024 | Legacy applications | Also considered insecure |
| Group 14 | 2048 | Secure communication | Standard for many modern protocols |
| Group 15 | 3072 | Enhanced security | Suitable for more secure applications |
| Group 16 | 4096 | High-security environments | Used when stronger security is needed |
| Group 17 | 6144 | High-security environments | Rarely used due to computational cost |
| Group 18 | 8192 | Very high-security environments | Used for extremely secure applications |
Each group is characterized by the following:
- Prime Modulus:
- A large prime number that determines the “space” within which the key exchange operates.
- The size of this prime (measured in bits) correlates with the security level of the key exchange.
- Generator:
- A base number that is used to derive the public and private keys.
- Security Level:
- The estimated strength against known cryptographic attacks.
The specific characteristics of the group influence the security and performance of the key exchange.
- Larger prime numbers generally provide more security
- But it also require more computational resources, affecting speed and efficiency.