Asymmetric Encryption

Updated Jan 30, 2024 ·

Overview

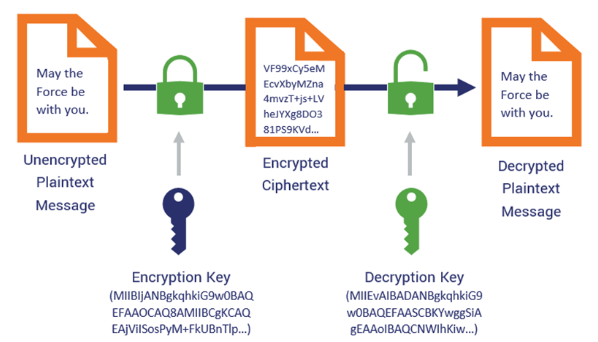
Asymmetric encryption uses a pair of keys: a public key for encryption and a private key for decryption.

• Public key encrypts data, and only the corresponding private key can decrypt it.
• Private key decrypts the data, can be used to sign data, which the public key can verify.

This dual-key system allows for secure communication, digital signatures, and secure key exchange without requiring shared secrets.

Advantages:

• No need to share the private key, reducing the risk of key compromise.
• Allows for digital signatures and public key infrastructure (PKI).

Disadvantages:

• Slower and more resource-intensive than symmetric cryptography.
• Less efficient for large amounts of data.

Digital Signature

A digital signature is a cryptographic method for verifying the authenticity and integrity of digital messages or documents. A private key is used to create the signature, which is then verified by the public key.

• Authentication: Confirms the identity of the signer.
• Integrity: Ensures the message hasn't been changed.
• Non-Repudiation: Prevents the signer from denying their signature.

Some use cases include:

• Email Encryption: Verifies email sources.
• Software Distribution: Confirms software integrity.
• Legal Documents: Validates digital contracts and agreements.
• Blockchain and Cryptocurrency: Secures transactions.

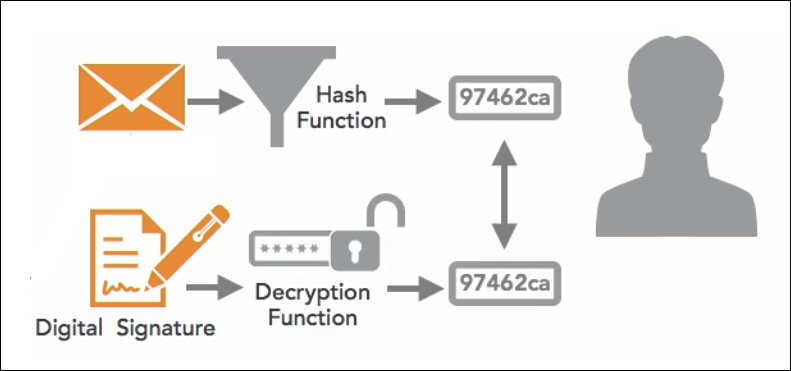
Creating a Digital Signature

1. Use the hash function to create a fixed-size hash from the message.
2. Use the user's private key to encrypt and sign the hash
3. This creates the digital signature.

Verifying the Digital Signature

Below are the steps to verify the digital signature:

1. Receiver gets the message and the digital signature.
2. Receiver uses the same hash function and the message to compute the hash value.
3. Receiver uses sender's public key to decrypt the digital signature
4. This results to the message digest.
5. Receiver compares the values from step 2 (hash value) and 3 (message digest).
6. If both values match, then the message is authentic.

How it looks like:

Encryption Methods

Each algorithm supports a range of key sizes that directly influence the security and efficiency of encryption and key exchange. Generally, larger key sizes offer more security but require more computational resources.

Algorithm	Key Structure	Supported Key Sizes	Use Cases	Strengths	Weaknesses
RSA	Public-private key pair	1024-4096 bits	Secure communication, digital signatures	Established, widely used; supports large key sizes	Slower than symmetric methods; susceptible to certain attacks with smaller keys
ECC (Elliptic Curve Cryptography)	Public-private key pair	160-521 bits	Secure communication, digital signatures	Smaller key sizes; heavily used in mobile devices	More complex mathematical basis; not as widely adopted as RSA
DSA (Digital Signature Algorithm)	Public-private key pair	1024-3072 bits	Digital signatures, authentication	Fast for signature generation; widely accepted	Slower for verification; requires secure parameter selection
Diffie-Hellman	Key exchange	1024-8192 bits	Secure key exchange, establishing shared keys	Enables secure key exchange over insecure channels	Does not provide encryption or authentication by itself

RSA

RSA is a widely-used public key encryption algorithm that provides secure data transmission. It relies on the mathematical difficulty of factoring large prime numbers, making it a robust choice for encryption and digital signatures.

• Utilizes a pair of keys: a public key for encryption and a private key for decryption
• Commonly used for securing sensitive data and establishing secure connections
• Supports digital signatures, ensuring data authenticity and integrity

RSA's versatility allows it to establish secure keys for encryption (confidentiality) and create digital signatures, ensuring message integrity and authenticity.

RSA versus DSA:

• RSA is the most widely used, compatible with a range of systems.
• DSA is optimized for digital signatures.

info

The RSA algorithm uses a trapdoor function, where encryption is easy to perform using the public key, but reversing the process (decryption) without the private key is challenging. RSA's principle is that certain mathematical operations are easy to perform, but their inverse operations are difficult without specific knowledge.

Merkle-Hellman Knapsack

The Merkle-Hellman Knapsack was one of the first public-key cryptosystems, inspired by the mathematical knapsack problem.

• Uses a sequence of numbers to encrypt data
• Decryption involves solving a mathematical subset-sum problem
• Relies on a super-increasing sequence* rather than large prime numbers

Although innovative at the time, it was proven ineffective after being broken in 1984, leading to its discontinuation in real-world use.

DSA

DSA is a federal standard for digital signatures, providing a method for verifying the authenticity and integrity of digital messages. Unlike RSA, it is not used for encryption but solely for creating digital signatures.

• Generates a digital signature to authenticate the sender of a message
• Relies on the discrete logarithm problem for its security
• Used in various applications, including email and software distribution

PGP and GnuPG

PGP (Pretty Good Privacy) and GnuPG (GNU Privacy Guard) are encryption programs used for securing emails and files. PGP was developed as a commercial encryption solution, while GnuPG is an open-source alternative that implements the OpenPGP standard.

• PGP

  • Combines symmetric and asymmetric encryption for enhanced security
  • Offers data encryption, decryption, and digital signatures
  • Widely used for securing email communications

• GnuPG

  • Open-source implementation of the OpenPGP standard
  • Provides compatibility with PGP and other OpenPGP-compliant systems
  • Available for various platforms, offering flexible encryption solutions

ElGamal

ElGamal is a public-key encryption system based on the Diffie-Hellman key exchange principle. It provides both encryption and digital signatures.

• Uses modular arithmetic and discrete logarithms for security
• Provides randomized encryption
• This produces different ciphertexts for the same message

ElGamal offers strong security but is slower and produces larger ciphertexts compared to RSA, which made it more suitable for specific cryptographic applications.

ECC

Elliptic Curve Cryptography (ECC) is an efficient, high-security encryption method used widely in modern, low-power devices.

• Primarily used in mobile and low-power computing devices
• Similar security with smaller key sizes, making it more efficient
• A 256-bit ECC key offers the same security level as a 2048-bit RSA key

ECC Variations

As mentioned previouosly, Elliptic Curve Cryptography (ECC) relies on the mathematical properties of elliptic curves to secure communications. Within ECC, there are several variations that offer different approaches and benefits.

• ECDSA

  • ECDSA (Elliptic Curve Digital Signature Algorithm)
  • Based on the Digital Signature Algorithm (DSA)
  • Creates secure digital signatures using elliptic curves
  • Used in secure communication, blockchain, and software signing
  • Uses smaller key sizes compared to RSA.
  • Efficient for generating digital signatures.

• ECDH

  • ECDH (Elliptic Curve Diffie-Hellman)
  • Based on the Diffie-Hellman key exchange
  • Establishes a shared secret key between parties
  • Provides a lightweight and secure way to exchange keys
  • Like ECDSA, requires careful parameter selection to ensure security.

• ECMQV

  • ECMQV (Elliptic Curve Menezes-Qu-Vanstone)
  • An elliptic curve-based key agreement protocol.
  • Used in situations requiring authenticated key exchange.
  • Adds authentication to key exchanges
  • Reduces computation compared to older MQV method
  • Less commonly used than ECDSA or ECDH.
  • Ddepends on correct parameter choices and secure implementation.

• EdDSA

  • EdDSA (Edwards-curve Digital Signature Algorithm)
  • A digital signature algorithm based on the Edwards curve family.
  • Used in modern cryptographic systems for digital signatures.
  • Resistant to several attacks, with rapid signature verification.
  • Relatively new, but gaining adoption due to its efficiency.

• Secp256k1

  • A specific elliptic curve used in ECC.
  • Widely used in blockchain and cryptocurrency, notably in Bitcoin.
  • Stronger security with smaller key sizes
  • Optimized for efficient computation.
  • Not widely used outside blockchain

Diffie-Hellman Key Exchange

Diffie-Hellman is a cryptographic protocol for secure key exchange which enables two parties to establish a shared secret over an insecure communication channel.

• Based on discrete logarithms and modular arithmetic.
• Shared secret can't derived easily by attackers due to complex math.
• An asymmetric algorithm, but doesn't provide the actual encryption.
• It is key exchange protocol, not an encryption algorithm.

Use Cases:

• Often used to set up shared encryption keys.
• Used when setting up VPN tunnels or other encryption tunnels.
• Applied in SSL/TLS, IPsec, and VPNs.

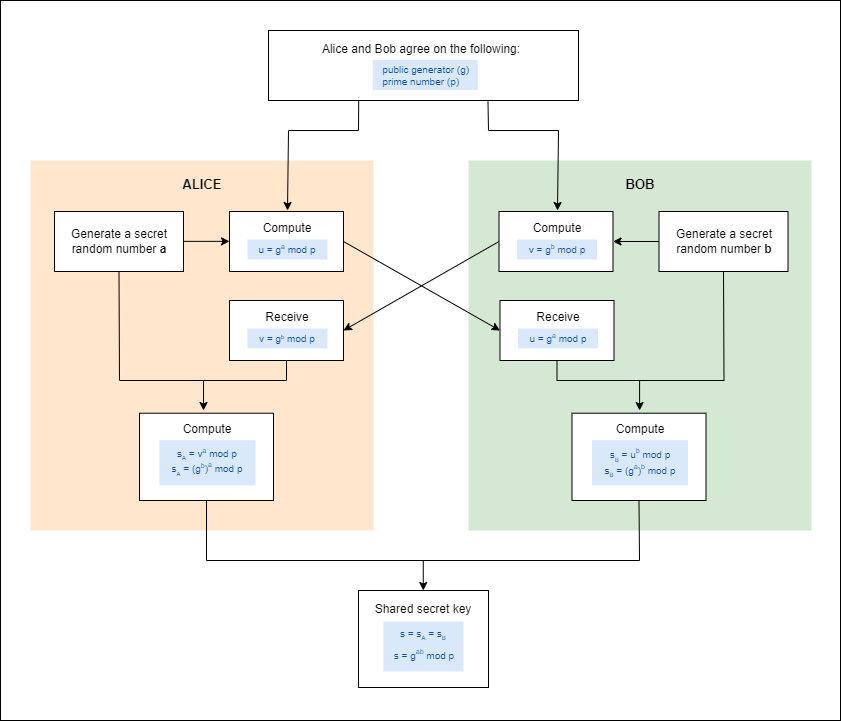
How It Works:

• Both parties agree on a base (generator) and a prime modulus.
• Each party chooses a private key.
• Public key is derived by raising the base to the power of the private key, modulo the prime.
• The public keys are then exchanged.
• Each party calculates the shared secret using the other's public key and their own private key.

Example:

• Parties agree on a common base ( g ) and a prime modulus ( p ).
• Alice chooses a private key ( a ) and sends ( g^a \mod p ) to Bob.
• Bob chooses a private key ( b ) and sends ( g^b \mod p ) to Alice.
• Alice calculates ( (g^b \mod p)^a ) to get the shared secret.
• Bob calculates ( (g^a \mod p)^b ) to get the same shared secret.

Strengths:

• Secure key exchange without revealing the key
• Resistant to eavesdropping and man-in-the-middle attacks when implemented correctly.

Weaknesses:

• Vulnerable to attacks like the man-in-the-middle if proper authentication is not implemented

• Depends on the difficulty of solving the discrete logarithm problem.

• To be truly secure, it should be combined with additional mechanisms

  

Diffie-Hellman Groups

Diffie-Hellman groups are pre-defined sets of parameters used in the Diffie-Hellman key exchange protocol. These groups consist of a generator (a base number) and a prime modulus, which are critical for the mathematical operations that allow two parties to create a shared secret.

Group Name	Prime Modulus Size (bits)	Typical Use Cases	Notes
Group 1	768	Legacy applications	Considered insecure, rarely used today
Group 2	1024	Legacy applications	Also considered insecure
Group 14	2048	Secure communication	Standard for many modern protocols
Group 15	3072	Enhanced security	Suitable for more secure applications
Group 16	4096	High-security environments	Used when stronger security is needed
Group 17	6144	High-security environments	Rarely used due to computational cost
Group 18	8192	Very high-security environments	Used for extremely secure applications

Each group has key components that define its security:

• Prime Modulus

  • A very large prime number defining the range for key operations
  • Larger modulus increases security but slows computation

• Generator

  • A base value used to create public and private keys
  • Ensures that the keys are mathematically linked yet unpredictable

• Security Level

  • Measured by how resistant it is to cryptographic attacks
  • Higher group numbers provide stronger protection
  • However higher group numbers require more processing power

The specific characteristics of the group influence the security and performance of the key exchange.

• Larger prime numbers generally provide more security
• Rrequire more computational resources, affecting speed and efficiency.

Quantum Cryptography

Quantum cryptography uses the principles of quantum mechanics to secure data and communications in ways that classical encryption cannot.

• Uses quantum particles to transmit information securely
• Attempt to intercept the data changes its state, alerting both parties

Researchers have already developed lab implementations of Quantum Key Distribution (QKD), which uses quantum properties to share encryption keys safely. Like quantum cryptography in general, QKD has not yet reached the stage of practical use.